【解答速報】2016年 開成中学校 算数(解説つき)大問4
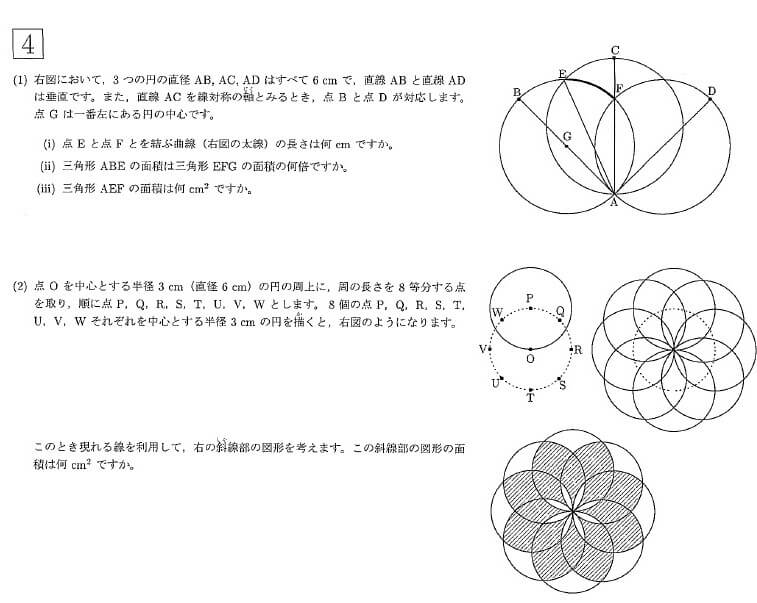
【4】
平面図形。
開成受験生なら(1)は3問とも正解したい。
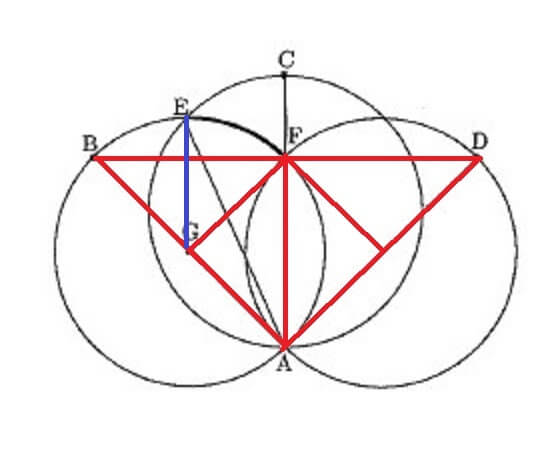
(1)まずは上図を参照してほしい。
(i)詳しい説明は省略するが、感覚的にも∠EGFが45°になるのはわかると思う。
6×3.14×45/360=2.355(cm)
(ii)△ABEと△EFGを比べる問題だが、△EFGと合同である△EBGと△ABEを比べることで一目瞭然。
高さが共通で底辺が2倍なので、答えは2倍。
(iii)△AEFは、底辺をAFと見た時、高さがBFの半分になっている。
では、底辺をAFと見た時に、高さがBFの三角形は?
→ABを斜辺とする直角二等辺三角形ABF である。
よって△AEFは、△ABFの半分の面積であるとわかる。
ABは円の直径なので6cm。よって6×3÷2=9(㎠)が△ABFの面積。
△AEFはその半分なので、9÷2=4.5(㎠)
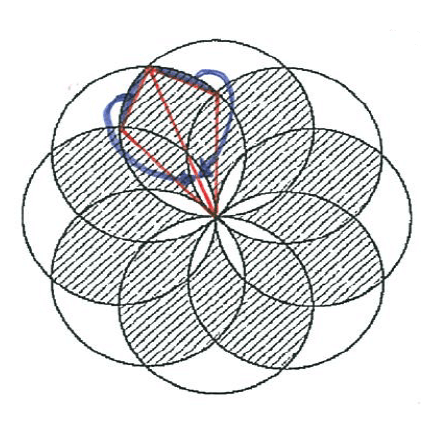
(2)下図参照。
このように等積移動すると、花びら8枚は赤い三角形2個×8の三角形16個に変身する。
そしてこの赤い三角形は、まさしく(1)の(iii)で求めた△AEFと合同な三角形。
よって、求めたい斜線部分の面積は 4.5×16=72(㎠) となる。
バックナンバー
(当時の速報なので粗い部分もありますが、読み物調で書いたので理解しやすい…かも!?)
駒込・巣鴨の塾・学習塾・個別指導 TESTEA駒込校
☎ 03-3942-5810
東京都文京区本駒込6-15-1 河西ビル4階
(受付時間:13時30分~22時 日曜日を除く)
テスティーの2016年合格実績はこちら!