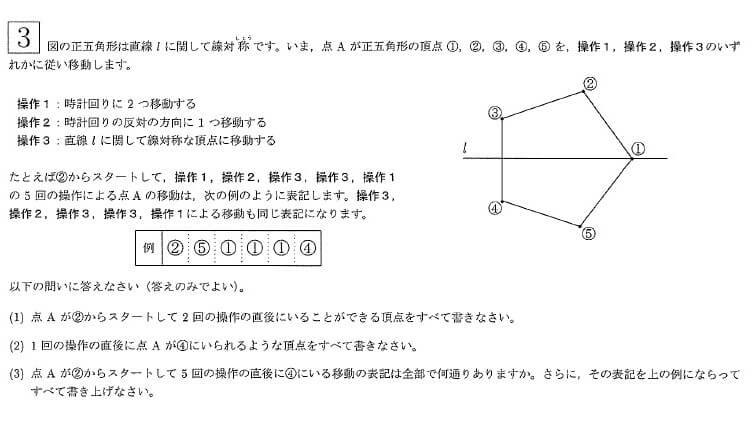
【解答速報】2016年　開成中学校　算数（解説つき）大問３

【３】
場合の数。
まずは問題文で定められているルールをしっかりと読むこと。
（１）（２）での失点は許されない。

（１）操作が3種類しかなく、2回の操作なので、たったの3×3＝9通りだけ考えればおしまい。
（1回目が操作1でも操作3でも⑤に行くので、実際にはもっと考えることは少なくて済む）
順番に丁寧に考えれば、　①②③④　とわかる。

（２）①～⑤のそれぞれから、1回で④に行けるかを検討するだけ。これも簡単。　①③　とわかる。

（３）　（１）と（２）が誘導になっている。
とはいえ調べるべきものは多く、慎重にやるにはかなり時間がかかる。

後回しにして部分点が取れればヨシとする、瞬間的な判断力が求められた問題と言えるのではないだろうか。

※編集注
あまりよい解き方が思いつかず、非常に読みづらい解説になっています。
「速報」ということでご容赦いただければと思います。 
（むしろ読み飛ばしてしまってください）

「②からスタートして5回の操作で④」
→②☆☆☆☆④（□だと味気ないので☆にしてみました）　ということ。

まず（１）で、②から2回の操作でいける頂点は①②③④とわかったので、

②☆①☆☆④
②☆②☆☆④
②☆③☆☆④
②☆④☆☆④

この4パターンが考えられる。

さらに（２）で、1回で④に行くには直前に①か③にいなくてはならないとわかったので、

②☆①☆①④
②☆②☆①④
②☆③☆①④
②☆④☆①④

②☆①☆③④
②☆②☆③④
②☆③☆③④
②☆④☆③④

この8パターンにわかれる。

あとは2つの☆に何が入るかをひとつずつ考えていけばよい。
（といっても、これが大変なのだが）

②☆①　→　②③①　か　②⑤①
②☆②　→　②⑤②
・・・・・
のように。

それらをすべて書き出すと（一応、上記8パターンの順に整理して書きました）、

②③①①①④
②⑤①①①④・・・例として印刷されているもの
②⑤②③①④
②⑤②⑤①④
②⑤③①①④
②③④③①④
②③④⑤①④
②③①②③④
②③①④③④
②⑤①②③④
②⑤①④③④
②⑤②⑤③④
②⑤③④③④
②③④②③④
②③④⑤③④