【解答速報】2014年 開成中学校 算数(解説つき)大問1、大問2
こんにちは! 下高井戸・久我山・西永福の個別指導塾TESTEA(テスティー)塾長、繁田和貴です。
開成番長ということで、平成26年度の開成中算数の解説をいち早く作成してみました。
解答は四谷大塚さんやインターエデュさんに載っていますが、解説が無いようだったので。
長くなるので、3つの記事にわけます。
まずは其の1として、大問1、大問2の解説です。
大問1、大問2の問題と解答はこちら(インターエデュのサイトです)
<以下、解説です>
【1】 (1)問題文中には公約数とあるが、本質は公倍数の問題。非常に易しい。
条件を見れば、21はアの約数、98もアの約数とわかる。 言い換えると、アは21の倍数でもあり、98の倍数でもある。つまりアは21と98の公倍数である。 同様に、イは21と35の公倍数、ウは35と98の公倍数である。
それぞれ最小公倍数を出すと、ア=294、イ=105、ウ=490となる。
※これで正解なのだが、丁寧に詰めてみます。 アイウの合計が1000以下という縛りがあるので、とりあえず足してみると889。当然これはOK。 イを「最小」公倍数ではなく、もうひとつ上の公倍数である105×2=210にした場合も、ギリギリでアイウの合計は1000以下であるが、ア294との最大公約数が42になってしまったり、ウ490との最大公約数が70になってしまったりするのでダメ。 これ以外のパターンはアイウの合計が1000を超えてしまうのでダメ。
(2)あまり見慣れない形だが、要素を分解するとたいしたことはない問題。正解したい。
まず、「あ」と「い」の大きさの比を求める。 「あ」の半径は「い」の半径の3倍なので、中心角が仮に同じなら、弧の長さも3倍になる。しかし実際には5倍なので、「あ」の中心角は「い」の中心角の5/3倍であるとわかる。 →あ:い=5:3 となる。
次に、「あ」と「い」の和を求める。方法はいくつかあるが、ここでは外角定理を使う方法を紹介する。 外角定理より、 あ=∠A+∠C い=∠A+∠B なので、 あ+い=∠A+∠A+∠B+∠C=20°+180°=200° となる。 5:3に比例配分して、「あ」=125°(エ) 「い」=75°(オ) である。
これがわかれば カ は計算するだけ。 途中で少し汚い分数が出るが、3.14でくくり出して計算すれば30×3.14=94.2 きれいな答えになる。
★「あ」と「い」の和を求める方法として、他にCを通りABに平行な補助線を引く方法も紹介しておきたい。この補助線の左端の点をDと名付ける。
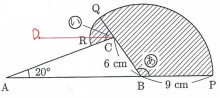
「い」は、∠DCAと∠DCQを合わせた大きさだが、まず∠DCAは∠BACと錯角で20°。 残りの∠DCQは、「あ」と合わせてちょうど一直線分180°とわかる(∠ABCと同位角なので)。 つまり「あ」と「い」の和は20+180=200°となる。
【2】開成対策をしていれば容易に正解できる。落としてはいけない問題。
(1)省略 くれぐれも書く方向(見る方向)を間違えないように。
(2)直方体から同じ形の三角すい台を2つ取っただけ。 三角すい台は、大きい三角すいの先っぽ4分の1を切り取った形なので、相似の立体の体積比を使うのが楽でしょう。 相似比1:4→体積比1:64なので、三角すいPEFHを63/64すれば三角すい台が求まる。 三角すいPEFHは、4×2÷2×4÷3=16/3 三角すい台は16/3×63/64=21/4 直方体は4×4÷2×6=48 よって 48-21/4×2=37.5 となる。


