【解答速報】2015年　開成中学校　算数（解説つき）大問４

（2016年2月1日更新：2016年度開成中算数の解答・解説速報も作成しました→2016年度開成中算数　解答速報　解説つき）

（問題はこちら→四谷大塚さんのサイトです）

【４】
立体図形（立体切断）の問題。
【３】までに時間をとられた受験生は、各点を表す文字が32個も登場し、一見複雑に見えるこの問題に焦ったかもしれない。
しかし開成受験生であれば、（１）はもちろん、（２）（３）まではぜひ正解したいところ。

（１）底面が2×2の正方形、高さが6cm　これはカンタン。
2×2×6＝24（㎤）

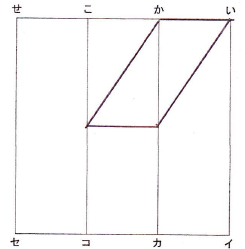
（２）切断面の上辺が「いか」であるのはよいとして、下辺がどこに来るのかを見定める問題。
細かい解説は省略するが、い、せ、セ、イで切るということは、「おソ」も、「あサ」も、ちょうど真ん中の位置で切られるということに気づいてほしい。

形さえわかれば、面積は、
2×3＝6（㎠）　と容易にわかる。

（３）（２）がヒントになっている。
与えられた8点を結んでできる直方体は、（２）の切断に加え、う、そ、ソ、ウで切ったときにできる真ん中の立体。（２）で求めた切断面の図形を底面とし、高さが2cm（「セソ」にあたる部分が高さ）の、斜めに傾いた角柱となる。
体積は、
6×2＝12（㎤）　となる。

（４）立体切断の練習をしてきた開成受験生でも、この問題はやや難しい。

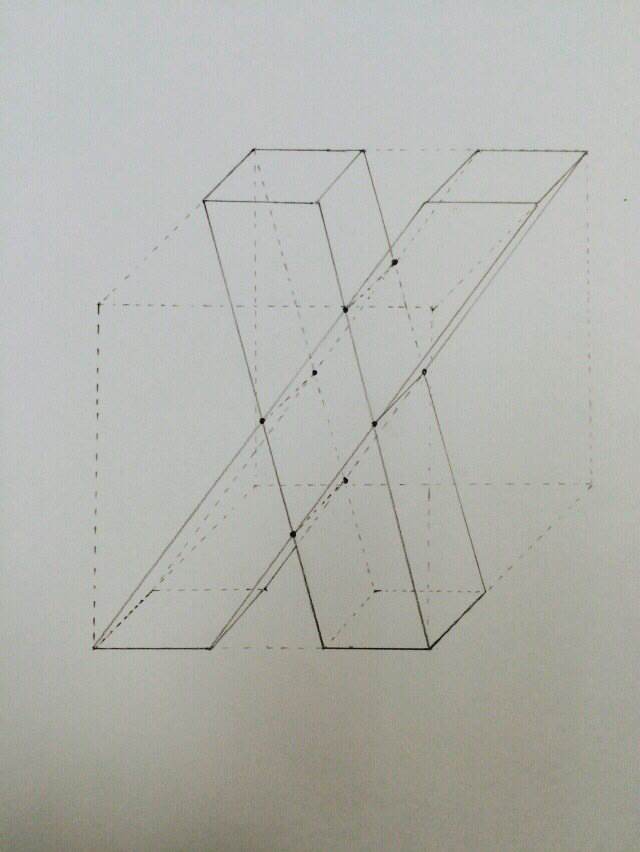
速報につき急いで手書きでかいたため見づらくて恐縮だが、以下の図の8つの「・」を頂点とする立体になる。

こちらも細かい解説は省略するが、手前側の斜めのひし形は、面「おくタス」を取り出し、そこに平行四辺形「おかタソ」と「きくセス」をかいてみるとイメージしやすいと思う（重なった部分のひし形）。奥側の斜めのひし形も同様。
要は変形した四角柱なのだが、この体積は、「けお」の中点と「しく」の中点を結んだ線で立方体の底面に向かって垂直に切ったときにできるAとBの共通部分のひし形　3×2÷2＝3（㎠）　を底面と見たとき、高さが2cmとなるので、
3×2＝6（㎤）と求めることができる。