【解答速報】2015年　開成中学校　算数（解説つき）大問２

（2016年2月1日更新：2016年度開成中算数の解答・解説速報も作成しました→2016年度開成中算数　解答速報　解説つき）

（問題はこちら→四谷大塚さんのサイトです）

【２】
見慣れた形の平面図形。
しかしいつもと違ったアプローチ。
図形的に解くか、式的に解くか。解法は１通りではない。
分析力と思考力が求められる問題。
（４）の最後がやたら簡単だったりするので、途中の考えづらい問題たちにハマらないのが肝心。
おそらく差がついた問題だろう。
取るべきところを確実に取る、わからないところはいったん飛ばして大問【３】【４】に取り掛かるなどの冷静な判断をしたい。

（１）ウォーミングアップ。㋔の中心角が30°になるのは受験生にとっては常識。
㋕＝㋔×２－㋓×１

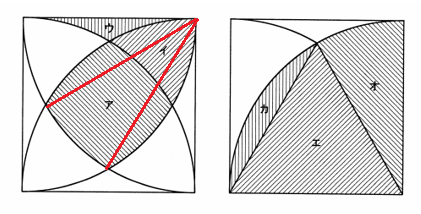
（２）㋐＋㋑＝㋕×２＋㋔＝（㋔×２－㋓×１）×２＋㋔＝㋔×５－㋓×２
（以下の図を参照）

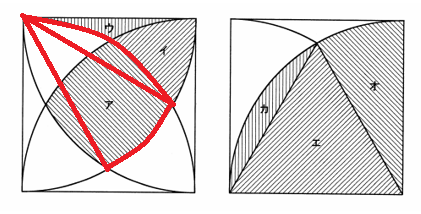
（３）㋑＋㋒＋㋔←これに㋕を加えると、㋓＋㋕の形になる（以下の図を参照）
よって、㋑＋㋒＋㋔＝㋓

（４）
㋐＝　の問題
まず図形的にとらえると、
㋐＝㋖×１－（㋑＋㋒）×４
㋑＋㋒＝㋔－㋕　　　　　　とわかる。

㋐＝㋖×１－（㋑＋㋒）×４＝㋖×１－（㋔－㋕）×４
＝㋖×１－㋔×４＋㋕×４

㋕を、（１）で求めた　㋕＝㋔×２－㋓×１　で置きかえると、
㋖×１－㋔×４＋㋕×４＝㋖×１－㋔×４＋（㋔×２－㋓×１）×４
＝㋖×１－㋔×４＋㋔×８－㋓×４＝㋖×１＋㋔×４－㋓×４

㋑＝　の問題
（２）で求めた　㋐＋㋑＝㋔×５－㋓×２　から、
㋑＝㋔×５－㋓×２－㋐　とわかる。

さらに（４）の㋐＝　の問題から、㋐＝㋖×１＋㋔×４－㋓×４　なので、これを上の式に入れると、
㋑＝㋔×５－㋓×２－（㋖×１＋㋔×４－㋓×４）＝㋔×５－㋓×２－㋖×１－㋔×４＋㋓×４＝㋓×２＋㋔×１－㋖×１

㋒＝　の問題
㋒＝㋖－㋓×１－㋔×２←図を見て一目瞭然

※（４）の㋐と㋑は、少々式処理がテクニカルなので、もう少し簡単な解法がないか検討中