【解答速報】2016年 開成中学校 算数(解説つき)大問1
※1より大きい分数は便宜上、仮分数で表記しています(例:7分の40→40/7)
【1】
割合で考える速さの問題。
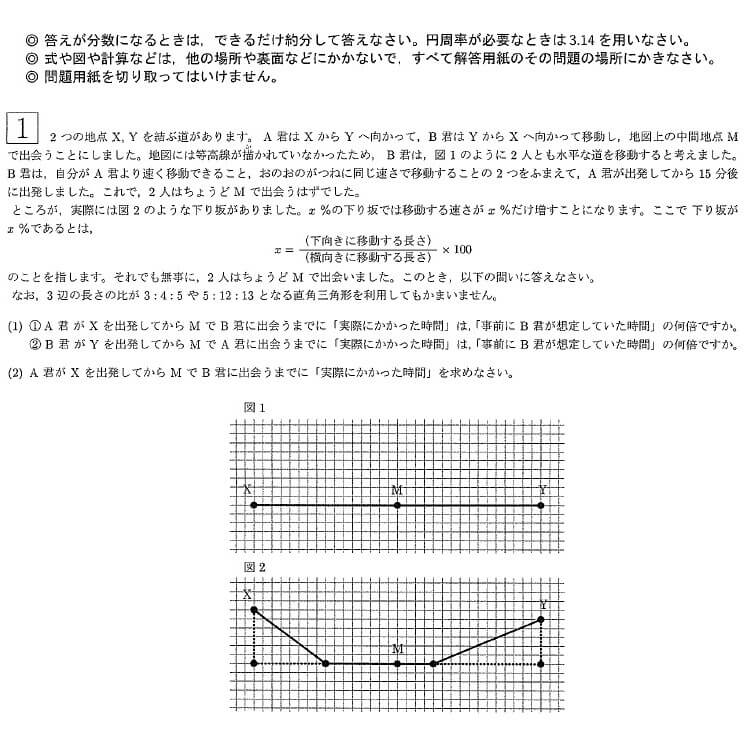
図1におけるXM(=YM)の距離を、マス目の数16とおいて考えてもよいし、1とおいてもよい。
今回は、とりあえず図1のXMを16とおいて考える。
いずれにせよ、図2になったときに「距離」「速さ」を勘違いしないよう、問題文の設定を正確に読み取り、慎重に考えることが大事。
(1)①事前にB君が想定していた時間→A君が図1のXMを移動するのにかかる時間
A君が図1のXM(水平な道)を移動するときの速さを1とする。すると、16÷1=16の時間がかかる(事前の想定)
実際には図2の道を進む。これを水平部分と、下り坂部分に分けて考える。
水平部分は距離8、速さ1。よって8÷1=8の時間がかかる。
慎重に考えたいのは下り坂部分。
距離は、問題文でも与えられている3:4:5の直角三角形を利用し、8×5/4=10
速さは、問題文の条件「x%の下り坂では~~」の部分から、6/8×100=75%増しと考えられるので1.75
よって下り坂部分は、10÷1.75=40/7の時間がかかる。
水平部分と合計すると、8+40/7=96/7の時間がかかる(実際)
「実際にかかった時間」は、「事前にB君が想定していた時間」の何倍かと聞かれているので、 96/7÷16=6/7(倍)が答えとなる。
②解説は省略気味に書きます。
図1におけるYM間の距離を16、B君の速さを1として、①と同じように考えればよい。
すると図1では16の時間、図2では224/17の時間がかかると計算できるので、
224/17÷16=14/17(倍)が答えとなる。
(2) (1)では、便宜上A君もB君も速さを1とおいたため、いずれも図1の時間が「16」と出たが、A君とB君の実際の速さは違うので、実際にかかった時間は同じではない。
そこで、A君の図1での時間を□1、B君の図1での時間を△1とする。
B君はA君より15分後に出発してMで出会う予定だったので、
□1-△1=15分 ということになる(□1の方が△1より15分長い)
一方、実際にかかった図2での時間は、(1)で求めた答えより□6/7と△14/17と表せ、この場合も同時にMについたことからこれらの差も15分といえるので、
□6/7-△14/17=15分 このように表せる。
あとは消去算で考えてあげれば、答えを導くことができる。
A君の「実際にかかった時間」を聞かれているので、□6/7を求めればよい。
計算すると、135/2(分)となる。
解答用紙の聞かれ方に合わせて答えると、1時間7分30秒。
バックナンバー
(当時の速報なので粗い部分もありますが、読み物調で書いたので理解しやすい…かも!?)
駒込・巣鴨の塾・学習塾・個別指導 TESTEA駒込校
☎ 03-3942-5810
東京都文京区本駒込6-15-1 河西ビル4階
(受付時間:13時30分~22時 日曜日を除く)
テスティーの2016年合格実績はこちら!