國學院大學久我山中学校－2019年度算数大問2(7)回転体の体積－過去問解説
問題
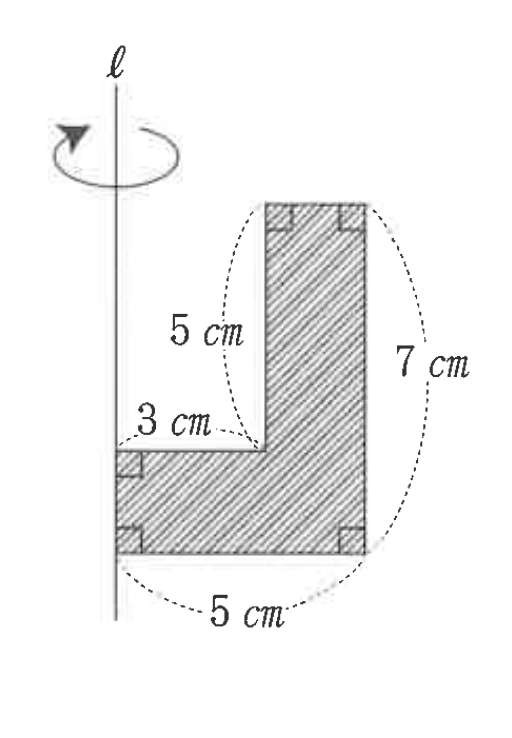
右の図の斜線がついた図形を直線ℓの周りに1回転させたときに出来る立体の体積は何㎤ですか。
解説
回転体の体積を求める問題としては、比較的易しいです。
回転した図形をイメージすると、大きい円柱から小さい円柱をくりぬいたような形になっているのが分かるので、そのように計算式を立てると、
\(（大きい円柱）-（小さい円柱）\)
\(=5 \times 5 \times 7 \times 3.14-3 \times 3 \times 5 \times 3.14\)
\(=(175-45) \times 3.14=408.2\)
となり、求める体積は408.2㎤とわかります。
答え：\(408.2cm^3\)
