【都立高校入試2023】数学　解説

本日は高校都立入試2023年の数学の解説を見ていきましょう。

ポイントになるのは大問４です。

【問1の解説】

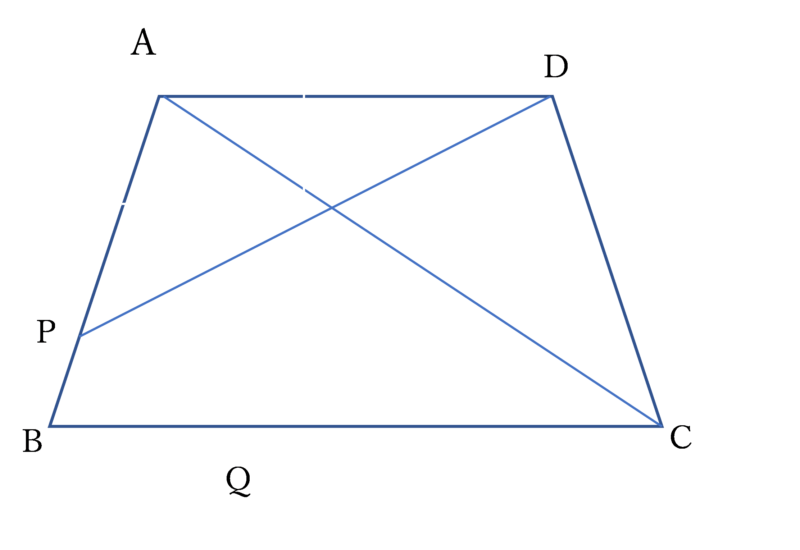
問1は、与えられた条件の下で∠ADPの大きさを求める問題です。

まず、∠AQC＝110°と与えられているので、∠AQB＝180°－110°＝70°であることがわかります。また、∠AQBと∠DAQは平行線の錯角の関係になっています。よって、∠DAQも70°であることがわかります。

ここで、四角形AQCDに注目してみましょう。与えられた条件から、AD∥QC、AQ∥DCであり、四角形AQCDは平行四辺形だとわかるので、AQ＝DCです。また、AB＝DCという条件があるので、AB＝AQとなります。

よって、三角形ABQはAを頂点とする二等辺三角形となっていることがわかりました。ゆえに、∠BAQ＝180°－（70°×２）＝40°と求められます。

さらに、⊿APDに着目すると、∠ADP＝180°―（∠DAQ＋∠BAQ）－α°＝180°―（70°＋40°）－α°となるので、∠ADP＝（70－α）°と求められました。よって答えはウです。

 

【問2①の解説】

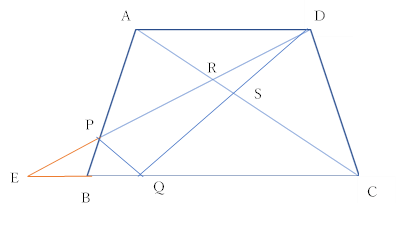
二つの三角形が相似であることを示す問題です。

まず、今回の問題の条件では、辺の長さの比は与えられていないので、「二組の角がそれぞれ等しい（二角相等）」という相似条件を使って証明することになります。相似を示したい二つの三角形⊿ASDと⊿CSQは、砂時計の様な形になっていますよね。ABCDは台形なので、AD∥BCです。よって、平行線の錯角の関係が利用できそうです。しかも、頂点Sで、直線ACと直線DQが交わっているので、対頂角は等しいという性質も利用できます。つまり、3つの角のどれを選んでも、意外とすんなり証明できてしまいます。どの角を選んでも良いのですが、今回はせっかくなので、錯角と対頂角を両方用いた証明の記述例を以下に示します。

【証明】

⊿ASDと⊿CSQにおいて対頂角は等しいので

∠ASD＝∠CSQ・・・①

AD∥BCより平行線の錯角は等しいので

∠ADS＝∠CQS・・・②

よって①、②より二組の角がそれぞれ等しいから

⊿ASD∽⊿CQS　（証明終）

 

【問2②の解説】

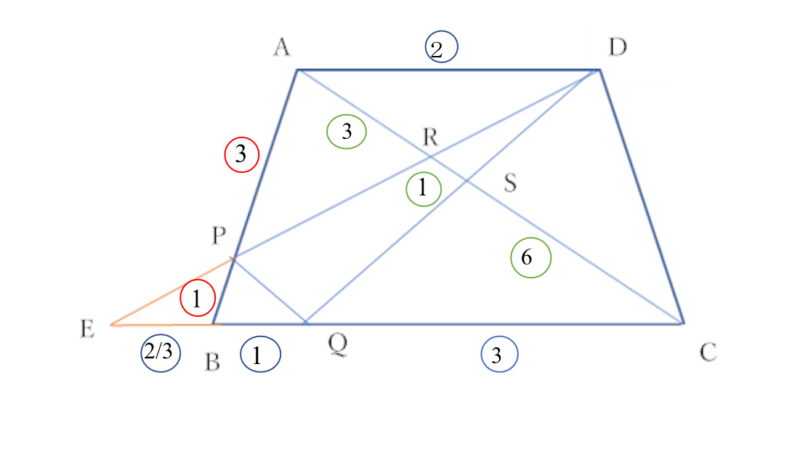
この問題は、辺の比を用いて最後まで計算を進めていく必要があります。また、適切に補助線を引けるかどうかがポイントです。

 

AP：PB＝３：１、AD：QC＝２：３、AC∥PQ

 

まずは、AD：QC＝２：３と分かります。問2の①で⊿ASD∽⊿CQSを示したので、AS：SC＝２：３・・・①だと分かります。

また、AC∥PQなので、平行線の性質よりAP：PB=CQ：QB＝３：１と求められます。

ここで、補助線を引くために直線DPと直線CBの交点をEとします。

EBをｘと置くと、AD：EB＝AP：PB、つまり２：ｘ＝３：１となります。

比の式を解くと、ｘ＝２/３と求めることができます。

 

＜平行線に注目する＞

続いて、ＡＤとＥＣの平行線に注目すると、ＡＤ：ＥＣ＝２：2/3＋１＋３＝２：１４/３なので、比を簡単にすると、ＡＤ：ＥＣ＝３：７です。

また、AD∥ECの平行線の性質を用いると、AD：EC＝AR：RC＝3：7・・・②と分かります。

ここで①、②の式を用いると、AR：RC：SC＝３：１：６・・・③ですね。

また、最初の台形ABCDに注目するとAD：BC＝１：２です。

⊿BACの底辺を辺BC、⊿DACの底辺を辺ADとみれば、⊿BACと⊿DACの高さは等しいので

台形ABCDと⊿DACの面積比は２：１・・・④となり、⊿ADC＝１/３四角形ABCDであるとわかります。

ここで③より、RS＝１/10ACですね。

⊿DACと⊿DRSは高さが等しいので面積比は10：1・・・⑤だと分かります。

よって④、⑤より⊿DRSの面積は台形ABCDの面積の1/30倍であると求めることが出来ました。したがって、「お」には1、「か」には3、「き」には0が入れば正解です。