【都立高校入試2023】理科　大問6解説

受験生の皆様お疲れ様です！テスティー下高井戸校の石川です。

先日の都立高校受験はどうでしたでしょうか？受験生の皆さんにとって自分が納得できる結果が出ていることを心より望んでいます。

さて、今回の話題ですが都立高校入試理科の簡単な講評と一部問題の解説についてです。

 

 

目次

　①都立高校入試理科の講評

　②大問6の解説

 

 

【都立高校入試理科の講評】

都立入試の理科は平均点からもわかる通り、難易度が安定していない印象をうけます。

今年度に関しましては昨年度よりもやや難化した印象を受けました。

しかしながら、難化だろうとそうでなかろうと基本的にやる勉強に関しては変わらないのかなと考えます。

基礎知識がちゃんと理解でき、おぼえているか、そのうえでの過去問演習により得点率をあげられるかがやはり重要であるといえます(他の人も同じことを言っていると思いますが…)。

間違えた問題を適当にやりすごしていませんか？『あ、これはケアレスミスだから次回気を付ければ大丈夫。』と思っているうちは成績が伸び悩むと思います。自分に厳しく頑張っていきたいものですね。

【大問6の解説】

さてさて、問題解説の方に移りたいと思います。今回は大問６の電気回路を扱います。

問題を以下に載せますので、是非ご覧ください！

　　　　　　　　

　　　　　　　　

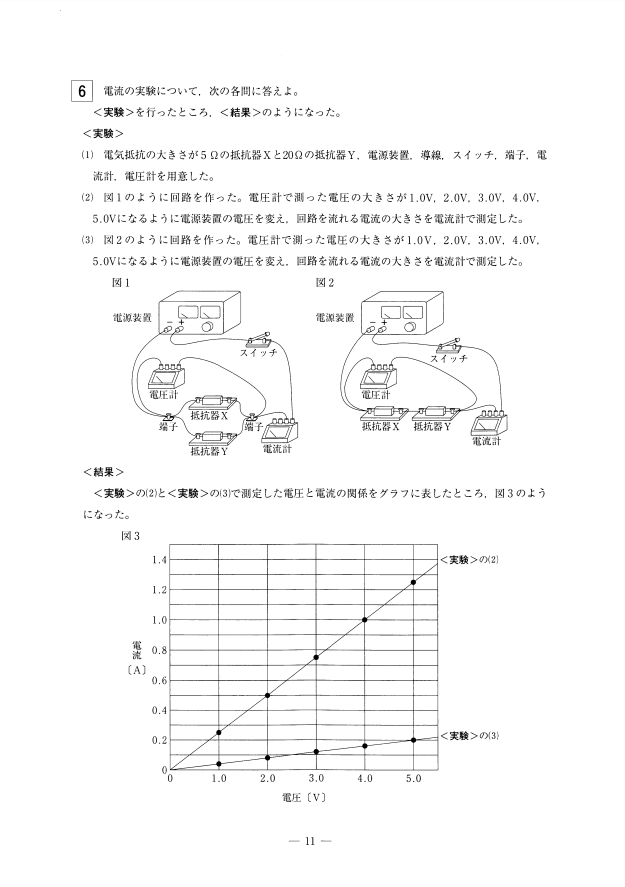
内容としましては並列回路と直列回路の電圧特性に関する話でした。それでは問１よりみていきましょう。

＜問1の解説＞

問１で重要なのはグラフをきちんと読み取れるか、というところです。

与えられたグラフはV-Aグラフですから、電流値がどのように増加しているかを読み取れれば問題ありませんね。

グラフより、電圧に対し電流が流れやすいのは図１の回路であることがわかりますので、イ、エは消去されます。

図１は並列回路ですから、各抵抗器にかかる電圧は等しく、図２は直列回路ですから抵抗器Xにかかる電圧は、抵抗器Yの分の電圧降下を受けます。

したがってウも消去され、アが正解となります。

 

＜問2の解説＞

続いて問２をみていきましょう。

問２もやはり、グラフが読み取れるかが勝負の分かれ目になるといえます。

回路の抵抗値を求めようとしてそのまま傾きだけ求めてしまうと実は抵抗値ではなく、引っかかってしまう落とし穴があります(V-Aグラフにおける傾きはコンダクタンスといいます)。

単位について理解があれば、[A/V]となったときに抵抗の逆数だな、と分かりますね。

これらを踏まえますと、図１の抵抗値は4[Ω],図２の抵抗値は25[Ω]となりますので、抵抗Xの抵抗値と比較しますと、ウのB<A<Cが正解となります。

 

＜問3の解説＞

続いて問３をみていきましょう。

問３で重要なのは電力の定義を覚えているか、というところにあります。

電力とは単位時間あたりに電流がした仕事量の事をさしますから、電圧をV[V]電流をI[A]と置きますと電力ＰはP=IV[W]とあらわすことができます。

これとグラフを踏まえると２：１となり、ウが正解となります。この問題はやや難しかったのではないでしょうか。

 

＜問4の解説＞

それでは最後に問４をみていきましょう。

問４で重要なのは先ほどの電力と、電力量の関係についてです。

電力は先ほども書いた通り「単位時間当たり(一秒間あたり)」の仕事量でした。一方で電力量は電流がした仕事量をさします。

つまり、電流がt[s]だけ仕事をしたら電力量はIVt[W・s]となりますね。

電力量は時間×電力と覚えておくとよいでしょう。

これを踏まえるとこの問題は、求めたい秒数をxとおくことにより方程式を立てれば直ぐに解ける問題となっています。完全なサービス問題ですね。

よって方程式を立てて解きますと、270[s]となりますから、正解はイの4分30秒となります。

 

これにて大問６の解説を終えたいと思います。今回は大問6のみの解説のみになってしまいましたが、他の大問についてもしっかり復習を行って、これからの学習に繋げてくださいね！