【中学受験】日常生活に潜む算数

こんにちは！

綱島・日吉の個別指導塾テスティー日吉校です。

 

さて、10月になりましたね。

ついに消費税が10％に引き上げられました。

消費税というとついつい間接税の説明をしたくなってしまうのは、きっと塾講師あるあるだと思うのです。笑

 

そういえば9月の終わりには駆け込み需要によりこんな風景を目撃しました！

これは日吉駅前にて増税前の定期券を買い求める行列の様子です。

これを見ると・・・算数の授業ができちゃいますよね。笑

 

まずは小学2、3年生レベルの授業だと、

「増税前の定期券購入のために駅の窓口に行列ができています。行列は1列17名で6列あります。さて、行列に並んでいるのは全部で何名いるでしょうか。」

こんな問題が完成しました！笑

まあ問題とも言えないぐらい簡単ですが、『全部で』という言い方をすると機械的に足し算をする子たちも中にはいるので、さりげなくそんなチェックが入っているのがポイントです！

 

 

ちなみに中学受験用に問題をつくるとこんな問題ができます。笑

「増税前の定期券購入のため、駅の窓口に102人の行列ができていて、1分に1人ずつ行列に加わっていきます。1つの窓口で1人が定期券を購入するのに2分かかります。現在窓口が6か所あり、どの窓口でも1人が購入にかかる時間が変わらないとき、この行列は何分でなくなりますか。」

 

 

どうでしょう。笑

せっかくなので、上記問題を解いてみましょう！

 

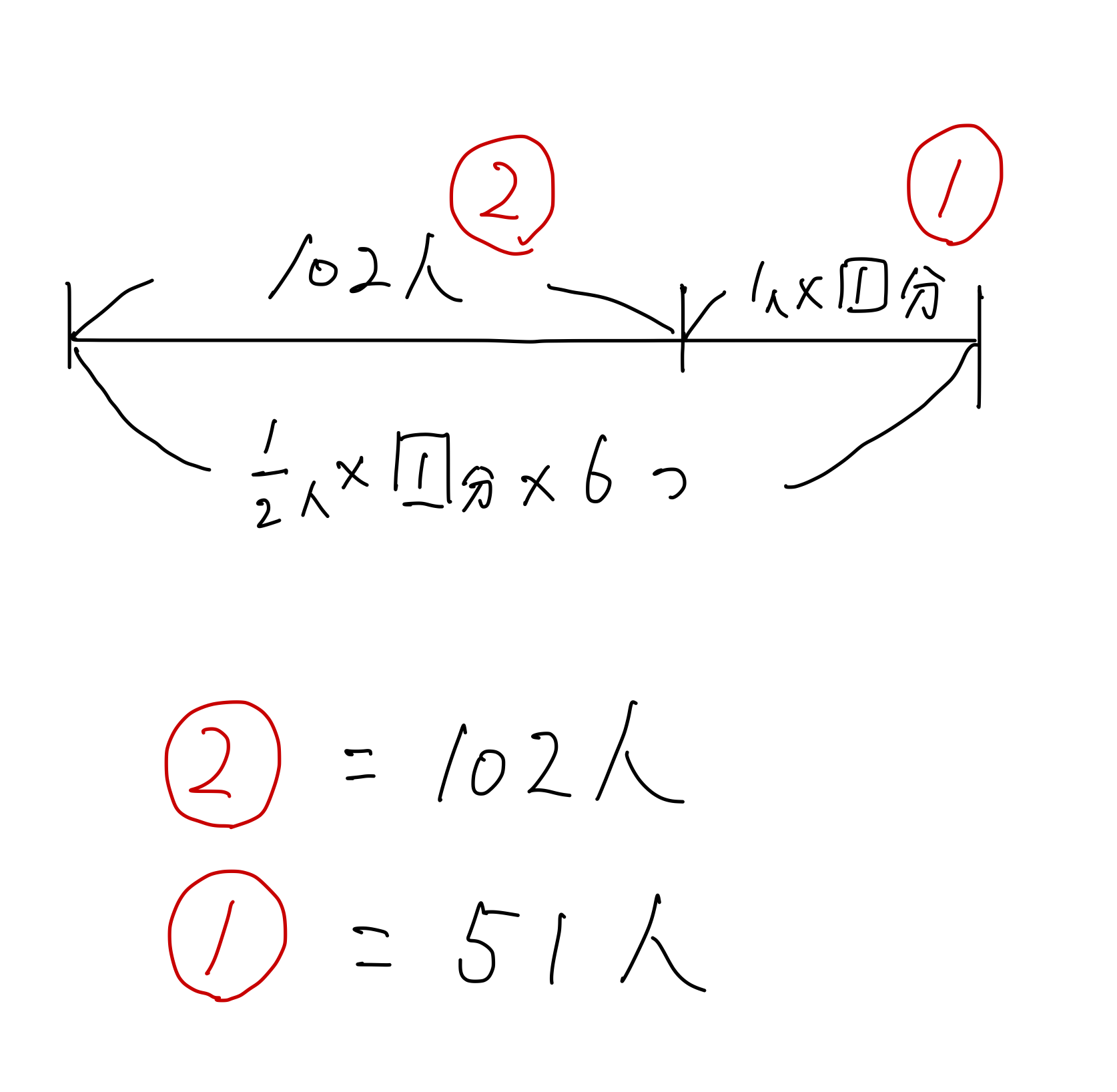
行列がなくなるまでにかかる時間を①分とすると

[mathjax]

$$102+1\times①=\frac{1}{2}\times6\times①$$

となります。

ちなみに上の式で出てくる

$$\frac{1}{2}$$

は1つの窓口で1分にさばける人数です。

 

 

では上記の式を解いてみましょう。

$$102+1\times①=\frac{1}{2}\times6\times①$$

$$102+①=③$$

$$①=102$$

$$①=51$$

よって今回の問題の答えは、51分となります！

 

つまりこの行列がなくなるのは51分後。

これを撮影したのが2019年9月30日20:00頃なので、21:00前までこの行列があったということが予想できます。（あくまで概算ですが。。。）

 

図を用いると、下記のようになります。

線分図に表すと非常にすっきりしますね。

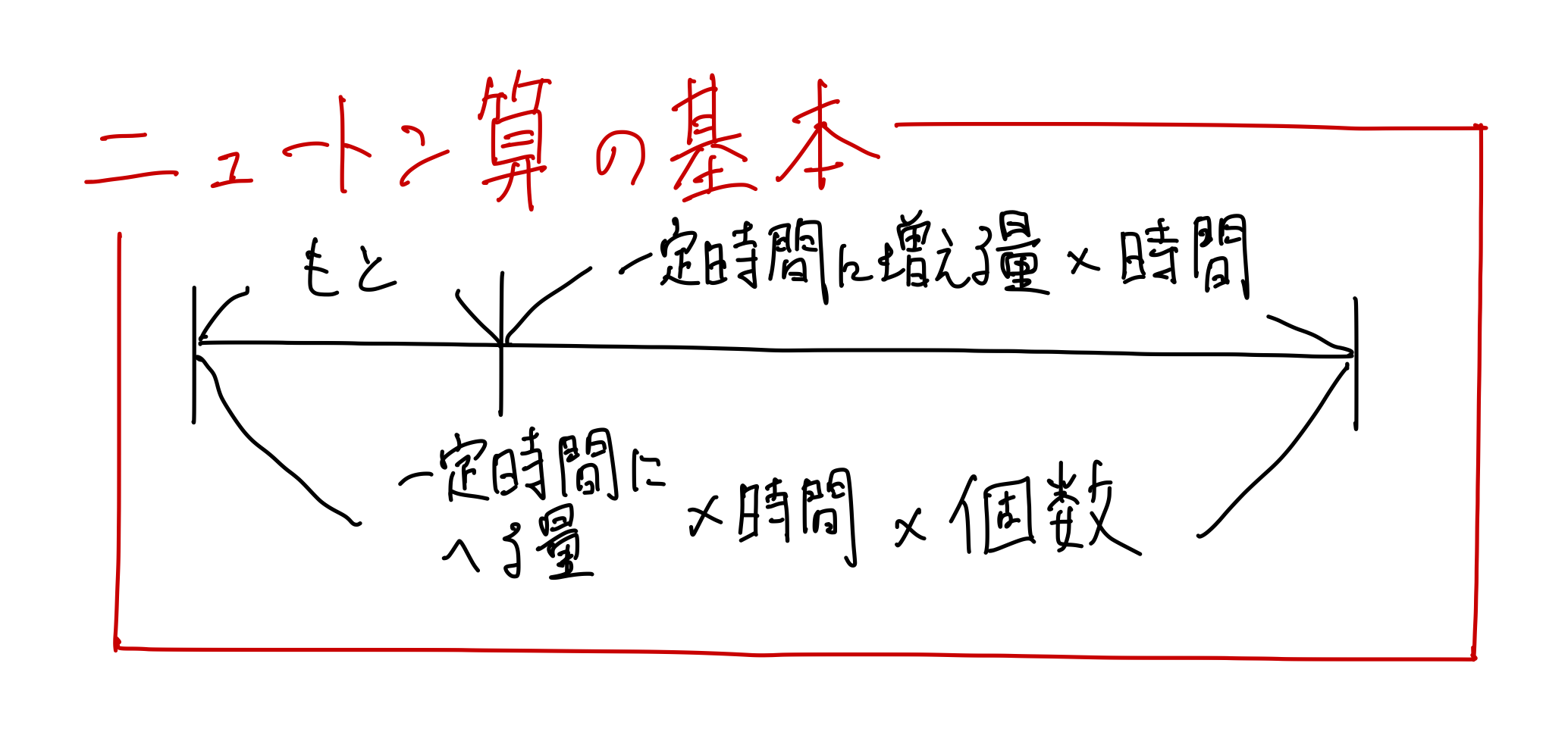
ちなみに今回の問題はいわゆるニュートン算の問題です。

 

せっかくニュートン算を扱ったので、今後もニュートン算に取り組みやすくするように解法を一般化して、よい問題演習ができるようにしましょう！

ニュートン算の基本は以下のようになります。

当たり前ではありますが、基本を分かったうえで問題演習をしていくと定着率が断然違いますよ！

 

本日は日常生活から算数の問題を考えてみました。

ちょっとしたことではありますが、こんな工夫で算数が好きになったりするので、ぜひ日常の何気ないワンシーンから算数やその他の教科を考えてみてください！